Square gyrobicupola
| Square gyrobicupola | |
|---|---|
| Type | Johnson J28 - J29 - J30 |
| Faces | 8 triangles 2+8 squares |
| Edges | 32 |
| Vertices | 16 |
| Vertex configuration | 8(3.4.3.4) 8(3.43) |
| Symmetry group | D4d |
| Dual polyhedron | - |
| Properties | convex |
| Net | |
In geometry, the square gyrobicupola is one of the Johnson solids (J29). Like the square orthobicupola (J28), it can be obtained by joining two square cupolae (J4) along their bases. The difference is that in this solid, the two halves are rotated 45 degrees with respect to one another.
The square gyrobicupola is the second in an infinite set of gyrobicupolae.
The 92 Johnson solids were named and described by Norman Johnson in 1966.
Formulae
The following formulae for volume and surface area can be used if all faces are regular, with edge length a:[1]
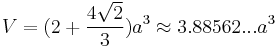
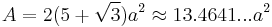
References
- ^ Stephen Wolfram, "Triangular gyrobicupola" from Wolfram Alpha. Retrieved July 23, 2010.
External links
- Weisstein, Eric W., "Johnson solid" from MathWorld.
- Weisstein, Eric W., "Square gyrobicupola" from MathWorld.